Irina – Simpson’s Paradox and segmentation: why analysis is crucial
What is Simpson’s Paradox?
Simpson’s Paradox refers to a data phenomenon where a trend existing in groups reverses when the data is studied as a whole. When it comes to analytics, understanding this paradox is vital since it can completely alter any insights gained from the data itself.
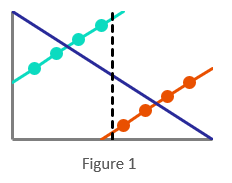
Figure 1. demonstrates two series’ of data (light blue and orange), each showing clear patterns. However, when the data is grouped together, the best fit pattern reverses (dark blue); a person on the black dotted line could have any of the three intersecting values. This has a huge impact on forecasting and reporting. Having no visibility of series is the same as not segmenting the data.
Simpson’s Paradox and segmentation: gender bias at UC Berkeley
An example of Simpson’s Paradox is an investigation into gender bias among students applying to the University of California. Male applicants were 44% successful compared to 35% of female applications. Surely such an obvious difference in success rates is evidence of favouritism on the part of the university?
Well, maybe. Dig a little deeper, however, and another possibility is revealed.
The table below holds the data for the largest 6 departments at UC Berkeley:

Here, the data shows that at department level, there’s actually very little evidence of bias towards men.
In fact, the largest ‘departmental bias’ occurs is in department A, where the female admission rate is 20% higher than the male. Further analysis of the variables indicates that men have better overall success rate because they apply to more lenient departments. As the table indicates, departments A and B have much higher admission rates than the other 4. These attract just 7% of female applications (from the top 6 departments), compared to 51% of male ones.
Another well-known example of Simpson’s Paradox is in the comparison of baseball batting averages, whereby a player can have a higher batting average than another across many seasons, but a lower one in each individual season.
Simpson’s Paradox and segmentation in business
I know what you’re thinking. How does the relationship between Simpson’s Paradox and segmentation apply in business situations?
Recently, I did some reporting for an arts venue which focused on how their sales have grown and what has driven that change.
Fig. 2 shows that the rise in sales was due to an increase in ticket prices.
Larger group size and frequency growth offset a decline in customer numbers (We’ll come back to that frequency growth shortly). So far, the obvious way to improve this sales growth would be to reverse that customer decline.
I then segmented data so the venue could use bespoke targeting on different customer types. They would receive tailored communications to improve each segment’s sales growth. This, in turn, would improve the total sales growth. Customers were split into New, Lapsed and Active. Active customers were grouped into past frequency bands 1 to 3 (increasing in order). The sales growth chart at segment level looked very different:

Fig. 3 shows that frequency growth had declined for every customer segment. In Fig. 2 we saw that frequency growth had grown for the whole. This is due to the increase in the proportion of customers who were Active and in higher frequency bands. These groups naturally have higher frequencies.

Conclusion
Segmenting the data groups for the arts venue showed an occurrence of Simpson’s Paradox. The total view suggested that frequency growth wasn’t a concern for the venue; in fact, each segment had declining frequency. Moving forward, the venue should act to counteract this trend.
Without segmenting the data to reveal underlying patterns, this information would have been invisible. The venue would only have found out about the low-level frequency decline much later, at a point when the trend would have been much harder to reverse.
References
1. https://homepage.stat.uiowa.edu/~mbognar/1030/Bickel-Berkeley.pdf
2. https://en.wikipedia.org/wiki/Simpson%27s_paradox
3. Ken Ross. “A Mathematician at the Ballpark: Odds and Probabilities for Baseball Fans (Paperback)” Pi Press, 2004. ISBN 0-13-147990-3. 12–13

